(%i1) define(f(x),sin(x));\[\mathtt{(\textit{%o}_{1})}\quad f\left(x\right):=\sin x\]
(%i2) a: -%pi$
(%i3) b: %pi$
(%i4) plot2d([f(x),diff(f(x),x,2)],[x,a,b]);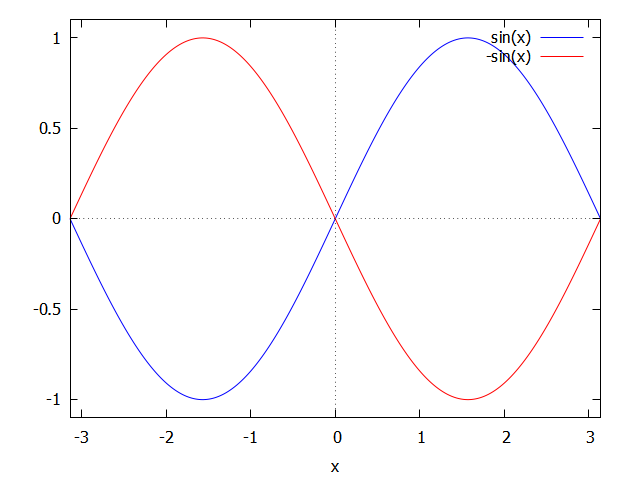
The objective of this lab is to deepen students’ understanding of the second derivative test and its application in analyzing the concavity and critical points of functions. By working through various examples, students will:
By completing this lab, students will gain practical experience in using the second derivative test to analyze the behavior of functions, enhancing their understanding of calculus concepts and their applications.
\(\displaystyle f(x)=\sin(x); \quad [-\pi,\pi]\)
\(\displaystyle f(x)=\frac{x^3}{x^2-1}; \quad [-7,7]\)
\(\displaystyle f(x)=x^x; \quad [0.2,1.5]\)
\(\displaystyle f(x)=x\cdot e^{-x}; \quad [0.5,4]\)
\(\displaystyle f(x)=3x^4-4x^3-6x^2+12x+1; \quad [-2,2]\)
\(\displaystyle f(x)=x^{2/3}(2-x); \quad [-3,3]\)
For the list of functions:
Sol a :
(%i1) define(f(x),sin(x));\[\mathtt{(\textit{%o}_{1})}\quad f\left(x\right):=\sin x\]
(%i2) a: -%pi$
(%i3) b: %pi$
(%i4) plot2d([f(x),diff(f(x),x,2)],[x,a,b]);
Sol b :
As can be observed in the plot:
the function has positive second derivative between \(-\pi\) and \(0\). - the function has negative second derivative between \(0\) and \(\pi\).
Sol c :
Because the second derivative is positive between \(-\pi\) and \(0\) then the function \(f\) has concavity up on that interval.
Because the second derivative is negative between \(0\) and \(\pi\) then the function \(f\) has concavity down on that interval.
Sol d :
Only one inflection point at \(x=0\) because the function change concavity from up to down at \(x=0\).
For the list of functions:
all critical points.Suppose \(f''\) is continuous on an open interval containing \(c\) with \(f'(c)=0\)
(%i5) load(to_poly_solve);\[\mathtt{(\textit{%o}_{5})}\quad \mbox{ C:/MAXIMA~1.0/share/maxima/5.47.0/share/to\_poly\_solve/to\_poly\_solve.mac }\]
(%i6) define(f(x),sin(x));\[\mathtt{(\textit{%o}_{6})}\quad f\left(x\right):=\sin x\]
(%i7) define(df(x),diff(f(x),x,1));\[\mathtt{(\textit{%o}_{7})}\quad \textit{df}\left(x\right):=\cos x\]
(%i8) define(ddf(x),diff(f(x),x,2));\[\mathtt{(\textit{%o}_{8})}\quad \textit{ddf}\left(x\right):=-\sin x\]
(%i9) a: -%pi$
(%i10) b: %pi$
(%i11) soln: to_poly_solve(df(x)=0,x);\[\mathtt{(\textit{%o}_{11})}\quad \textit{%union}\left(\left[ x=\frac{2\,\pi\,\textit{%z}_{472}+\pi}{2} \right] \right)\]
(%i12) candidates: [-%pi/2,%pi/2];\[\mathtt{(\textit{%o}_{12})}\quad \left[ -\left(\frac{\pi}{2}\right) , \frac{\pi}{2} \right] \]
(%i13) ddf(candidates[1]);\[\mathtt{(\textit{%o}_{13})}\quad 1\]
(%i14) ddf(candidates[2]);\[\mathtt{(\textit{%o}_{14})}\quad -1\]
Cell -> Insert Image).Shift+Enter in each code chunk.Ctrl+R.FINAL_Lab7_Calc1_YOURLASTNAME_mmddyy.wxmx.)pictures need to be in the same folder of your .wxmx file↩︎