(%i1) define(f(x),3*x^2-4*x+2);\[\mathtt{(\textit{%o}_{1})}\quad f\left(x\right):=3\,x^2-4\,x+2\]
Visualization of Critical Points Using First and Second Derivatives
The objective of this lab is to enhance students’ understanding of critical points and their significance in the analysis of functions. Students will achieve this by visualizing the behavior of functions and their derivatives. Specifically, students will:
Absolute Maximum and Minimum of a Function in an Interval
The objective of this section is to find the absolute maximum and minimum values of a function within a given interval. Students will follow a systematic procedure to locate and evaluate critical points and endpoints to determine these extreme values.
Plot on the same window, \(f(x),\,f'(x),\,f''(x)\) and then create a list with the \(x\)-values of the critical points for the following functions:
(%i1) define(f(x),3*x^2-4*x+2);\[\mathtt{(\textit{%o}_{1})}\quad f\left(x\right):=3\,x^2-4\,x+2\]
(%i2) soln: solve(f(x)=0,x);\[\mathtt{(\textit{%o}_{2})}\quad \left[ x=-\left(\frac{\sqrt{2}\,i-2}{3}\right) , x=\frac{\sqrt{2}\,i+2}{3} \right] \]
(%i3) fdf: diff(f(x),x,1);\[\mathtt{(\textit{%o}_{3})}\quad 6\,x-4\]
(%i4) sdf: diff(f(x),x,2);\[\mathtt{(\textit{%o}_{4})}\quad 6\]
(%i5) plot2d([f(x),fdf,sdf],[x,-10,10]);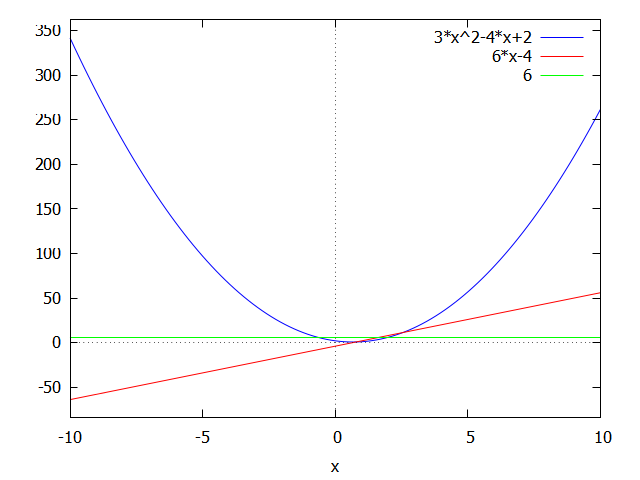
(%i6) plot2d([f(x),fdf,sdf],[x,0,2]);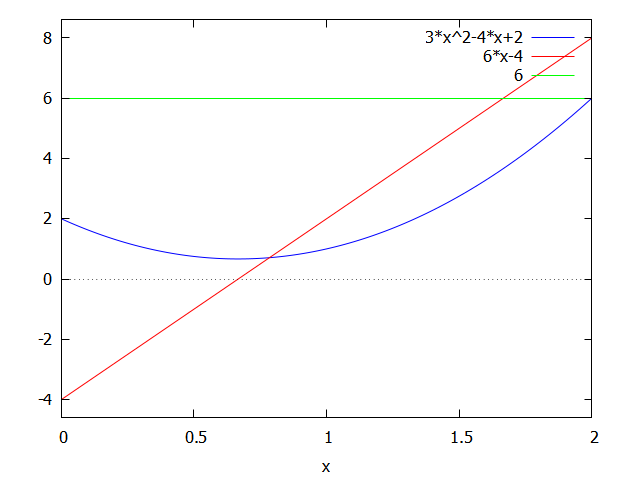
(%i7) cp: solve(fdf=0,x);\[\mathtt{(\textit{%o}_{7})}\quad \left[ x=\frac{2}{3} \right] \]
In this case we have a well behave polynomial function, therefore the derivative is also a well behave function, therefore you will not find critical points when \(f'=\inf\).
\(\displaystyle f(x)=\frac{x^3}{3}-9x\)
\(\displaystyle f(x)=3x^3+\frac{3x^2}{2}-2x\)
\(\displaystyle f(x)=x^3-4a^2x\)
\(\displaystyle f(t)=\frac{t}{t^2+1}\)
\(\displaystyle f(x)=\frac{e^x+e^{-x}}{2}\)
\(\displaystyle f(x)=\frac{1}{x}+\ln x\)
\(\displaystyle f(x)=x^2\sqrt{x+5}\)
Determine the location and value of the absolute extreme values of \(f\) on the given interval, if they exist. (Follow procedure discussed in class.)
(%i8) define(f(x),x^2-10);\[\mathtt{(\textit{%o}_{8})}\quad f\left(x\right):=x^2-10\]
(%i9) a: -2;\[\mathtt{(\textit{%o}_{9})}\quad -2\]
(%i10) b: 3;\[\mathtt{(\textit{%o}_{10})}\quad 3\]
(%i11) fdf: diff(f(x),x,1);\[\mathtt{(\textit{%o}_{11})}\quad 2\,x\]
(%i12) sdf: diff(f(x),x,2);\[\mathtt{(\textit{%o}_{12})}\quad 2\]
(%i13) plot2d([f(x),fdf,sdf],[x,a,b]);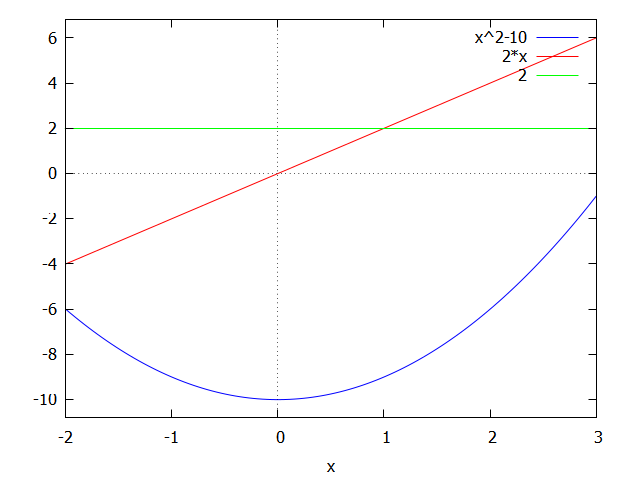
Locate the critical points \(c\) in \((a,b)\), where \(f'(c)=0\) or \(f'(c)\) does not exist.
(%i14) cpz: solve(fdf=0,x);\[\mathtt{(\textit{%o}_{14})}\quad \left[ x=0 \right] \]
(%i15) cpu: solve(fdf=inf,x);\[\mathtt{(\textit{%o}_{15})}\quad \left[ x=\frac{\infty }{2} \right] \]
Evaluate \(f\) at the critical points and at the end points of \([a,b]\).
(%i16) candidates: [f(a),f(rhs(cpz)),f(b)];\[\mathtt{(\textit{%o}_{16})}\quad \left[ -6 , -10 , -1 \right] \]
Choose the largest and smallest values of \(f\) from Step 2 for the absolute maximum and minimum values, respectively.
(%i17) sort(candidates);\[\mathtt{(\textit{%o}_{17})}\quad \left[ -10 , -6 , -1 \right] \]
Then the absolute minimum occur at \(x=0\), and the absolute maximum occur at \(x=b=3\).
\(\displaystyle f(x)=(x+1)^{4/3}\) on \([-9,7]\).
\(\displaystyle f(x)=x^3-3x^2\) on \([-1,3]\).
\(\displaystyle f(x)=3x^5-25x^3+60x\) on \([-2,3]\).
\(\displaystyle f(x)=\cos^2 x\) on \([0,\pi]\).
\(\displaystyle f(x)=\sin 3x\) on \([-\pi/4,\pi/3]\).
\(\displaystyle f(x)=(2x)^x\) on \([0.1,1]\).
\(\displaystyle f(x)=x^2+\cos^{-1}x\) on \([-1,1]\).