3 Lab 3: Derivatives

Objective

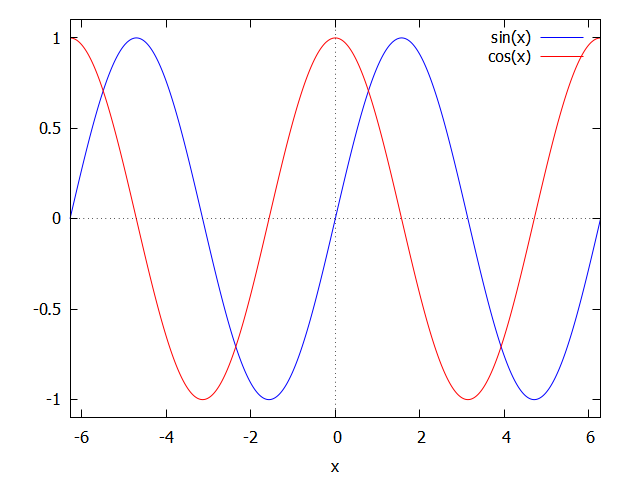
The objective of this lab is to explore and understand the concepts of slopes (derivatives) of trigonometric functions, as well as to practice applying derivative rules, such as the product and quotient rules, using both manual calculations and Maxima computer algebra system (CAS). Students will:

Visualize and Analyze Trigonometric Functions:
- Plot the functions \(\sin(x)\) and \(\cos(x)\) and observe their slopes at specific points.
- Analyze how the slopes of \(\sin(x)\) and \(\cos(x)\) change over given intervals.
Learn and Apply Symbolic Differentiation in Maxima:
- Understand how to use the diff function in Maxima for symbolic differentiation.
- Calculate the derivatives of various functions using Maxima and verify results.
Derive and Interpret Trigonometric Function Derivatives:
- Plot \(\sin(x)\) and its derivative, as well as \(\cos(x)\) and its derivative, to understand the relationships between these functions and their derivatives.
- Express the mathematical relationships between \(\sin(x)\), \(\cos(x)\), and their derivatives in equation form.
Practice Product Rule:
- Manually calculate derivatives using the product rule for given functions.
- Verify the manual calculations using Maxima and understand any discrepancies.
Practice Quotient Rule:
- Manually calculate derivatives using the quotient rule for given functions.
- Verify the manual calculations using Maxima and understand any discrepancies.
Develop Problem-Solving Skills:
- Solve additional derivative problems manually and using Maxima, reinforcing the learned concepts and techniques.

By the end of this lab, students will have a comprehensive understanding of the derivatives of trigonometric functions, proficiency in using Maxima for symbolic differentiation, and enhanced skills in applying the product and quotient rules to various functions.

3.1 Let’s study the slope at each point for \(\cos(x)\) and \(\sin(x)\) functions

Let’s plot the sin(x) and cos(x) function on the same window:

(%i1) plot2d([sin(x),cos(x)],[x,-2*%pi,2*%pi]);

focus at \(x=0\), what is the slope of \(\cos(x)\)? answer here:

focus at \(x=0\), what is the slope of \(\sin(x)\)? answer here:

Now do finite advance on \(x\), between 0 and \(pi/2\) and comment how the slope is changing for \(\cos(x)\). Answer here:

Now do finite advance on \(x\), between 0 and \(pi/2\) and comment how the slope is changing for \(\sin(x)\). Answer here:

3.2 function `diff(f(x),x,1)`

The function which do the trick on maxima is called diff, and have 3 arguments, the first is the function, second is the independent variable you are calculating the derivative, and third is how many times you want to differentiate, e.g. if you want to calculate twice the derivative of the function \(f(x)\) the maxima code is diff(f(x),x,2)

Lets try to calculate first the derivative of the following function : \[f(x)= x^5-\frac{1}{x^2}-2x -7\]

Using the power rule we know that \[f' = 5x^4 +\frac{2}{x^3} -2 \] easy-peasy !

How we use maxima to get the same answer?

Write what could be the code which calculate that derivative:

(%i2) define(f(x),x^5 -1/x^2-2*x-7);

\[\mathtt{(\textit{%o}_{2})}\quad f\left(x\right):=x^5-2\,x-\frac{1}{x^2}-7\]

(%i3) diff(f(x),x,1);

\[\mathtt{(\textit{%o}_{3})}\quad 5\,x^4+\frac{2}{x^3}-2\]

3.3 Let’s calculate the derivative of \(\cos(x)\) and \(\sin(x)\) functions using `maxima-cas`

Using what you learn on the previous section:

Plot \(\sin(x)\) and the derivative of \(\sin(x)\) on the same window.
Plot \(\cos(x)\) and the derivative of \(\cos(x)\) on the same window.
What are the relationships between \(\cos(x)\) and \(\sin(x)\) and its derivatives?
Type 2 equations which express this relationships.

3.4 Let practice the product rule

3.4.1 Example.

Calculate the derivative of \[y = \frac{x^3}{3} + x^2 + x + 3 \]

Do the following 7 steps on a paper, then take a screenshot and uploaded to the computer:

define who is \(f\) and \(g\)
calculate \(f'\) and \(g'\)
express the product rule for derivatives.
replace \(f'\), \(g\) and \(f\) and \(g'\)
cancel what could be cancel
factor what could be factor
frame your final answer in a box

Compare your results with what maxima can calculate by a couple lines of instructions:

(%i4) define(y(x),x^3/3 +x^2 +x +3);

\[\mathtt{(\textit{%o}_{4})}\quad y\left(x\right):=\frac{x^3}{3}+x^2+x+3\]

(%i5) diff(y(x),x,1);

\[\mathtt{(\textit{%o}_{5})}\quad x^2+2\,x+1\]

(%i6) factor(%);

\[\mathtt{(\textit{%o}_{6})}\quad \left(x+1\right)^2\]

It is the same? if not why not?

Note: To factor an expression using maxima you can use the command factor. % refer to the last output

3.4.2 Follow the same steps of previous example to calculate the following problems by hand and using maxima:

\[ y= x^2 \cdot 2^x \]
\[ y = \sqrt{x} \cdot (1-x^2)\]
\[ y = x^3 \cdot \sin(x) \]

3.5 Let practice the quotient rule

3.5.1 Example.

Calculate the derivative of \[y = \frac{x^2+3x+4}{x^2-1} \]

Do the following 7 steps on a paper, then take a screenshot and uploaded to the computer:

define who is \(f\) and \(g\)
calculate \(f'\) and \(g'\)
express the quotient rule for derivatives.
replace \(f'\), \(g\) and \(f\) and \(g'\)
cancel what could be cancel
factor what could be factor
frame your final answer in a box

3.5.2 Follow the same steps of previous example to calculate the following problems by hand and using maxima:

\[ y= \frac{x^2 +1}{x^2-4} \]
\[ y = \frac{x}{e^x}\]
\[ y = e^{-x}\]

3.6 For each of the previous sections:

take a picture of your handwritten work, submit them to the dropbox, and then also linked to the corresponding section of your wxmaxima document¹ (Cell -> Insert Image)
be sure your code run correctly by pressing Shift+Enter in each code chunk.
be sure the whole document display correctly, by running Ctrl+R
Submit on the corresponding Dropbox folder, with the corresponding name (FINAL_Lab3_Calc1_YOURLASTNAME_mmddyy.wxmx.)

pictures need to be in the same folder of your .wxmx file↩︎